Trends in survival of young adult patients with acute lymphoblastic leukemia in Sweden and USA
This page contains supplementary material for our letter published in Blood.
Table of Contents
Swedish Data
We identified all patients diagnosed with ALL between January 1st 1980 and December 31st 2015 in the Swedish Cancer Register. The Swedish Cancer Registry registers new diagnoses using the prevailing ICD version, but backcodes all registrations to ICD-7. We used ICD-7 code 204.0 to identify cases of ALL.
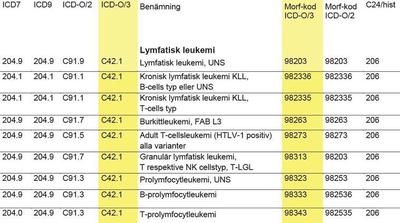
For 6 individuals registered as having multiple primary ALL in Sweden, we included only the first diagnosis. We did not exclude any patients on the basis of previous diagnoses of another cancer. Cases diagnosed incidentally at autopsy (n=19) or classified as non-malignant (n=2) were excluded from all analyses.
SEER Data
Using a case-listing session in the SEER*Stat software, we identified all patients diagnosed with ALL during 1973-2015 based on the SEER 9 database of the Surveillance, Epidemiology, and End Results (SEER) Program of the United States National Cancer Institute (12). Patients were followed up to the end of 2015.
In order to match the Swedish data, we set “multiple primary by international rules” to “yes” in the selection tab and specified “All Tumors Matching Selection Criteria / One Tumor per Statistic” in the multiple primary selection option in SEERStat. As with the Swedish data, we did not restrict to microscopically confirmed cases. All cases were classified as having malignant behaviour. No cases were classified as “death certificate only” or “autopsy only”. We only included the first diagnosis for the one individual registered as having multiple primary ALL. Expected survival was estimated in SEERStat using the table “U.S. 1970-2014 by individual year (White, Black, Other (AI/API), Ages 0-99, All races for other unspec 1991+ and unknown)”. Data on expected survival for Sweden (by age, year, and sex) was obtained from the Human Mortality Database (10), based on data from Statistics Sweden.
Files for reproducing the analysis of the SEER Data
Researchers can apply to access the SEER data by submitting a signed research data agreement. Below we provide the files and code to reproduce our analysis of the SEER data. The requirements are:
- Approval to use the SEER data (i.e., an approved research data agreement)
- SEER*Stat statistical software (available for free here)
- SAS (commerical software)
- Stata (commercial software)
The process is somehat convoluted. We prefer Stata for statistical analysis, but SEERStat exports data with a SAS data dictionary so we used SAS to add the variable labels and formats before exporting the data into Stata format for analysis. It’s possible to avoid the step requiring SAS, but one would need to rewrite some of the SAS code into Stata code. ASCII text versions of the SEER data are available, but we chose to extract the data as a text file using a SEERStata case listing session in order to use the tools available in SEER*Stat for selecting patients and for adding the population rates.
The procedure is as follows:
- Run the SEER*Stat case listing session (ALL_IARC_multiple-primary_rules.slm)
- Run this SAS code (ALL_IARC_multiple-primary_rules_clean_make_dta.sas) to perform some minor cleaning and create a Stata data set. SEER*Stat will create a .SAS file in the previous step. Do not use that file; use the .SAS file here which contains additional code.
- Run this do file (model_stpm2_cat_age.do) to fit the model and draw graphs in Stata
Parameterisation of the model
Following is an extract of the Stata code for preparing the data and fitting the model. The same code was used for both the Swedish and SEER data. The link to the complete code for modelling the SEER data is available here.
We start by creating the relevant variables. We chose to model age in categories, so create dummy variables. We chose to model year of diagnosis using restricted cubic splines, so create the spline basis vectors using the rcsgen command; 2 degrees of freedom corresponds to 1 internal knot (at the median) and 2 boundary knots. We store the value of df in a macro variable so that it is easier to compare different choices.
/*dummy variable for sex*/
gen female=sex-1
/* create dummy variable for agegroup */
quietly tab agegroup, gen(agegroup)
// df for spline variables for year of diagnosis
local df_yr 2
/* spline variables for year of diagnosis*/
rcsgen yeardiag, df(`df_yr') gen(yearspl) orthog
/* generate interaction variables */
forvalues yr=1/`df_yr' {
gen yearsexspl`yr'=yearspl`yr'*female
}
forvalues yr=1/`df_yr' {
gen ageyear1`yr'=yearspl`yr'*agegroup1
gen ageyear2`yr'=yearspl`yr'*agegroup2
gen ageyear3`yr'=yearspl`yr'*agegroup3
gen ageyear4`yr'=yearspl`yr'*agegroup4
}
We now stset the data, using the exit() option to censore at 72 months and fit the model.
stset stime, fail(status==1) id(id) scale(12) exit(t 72)
stpm2 yearspl* agegroup2 agegroup3 agegroup4 ageyear2* ageyear3* ageyear4*, ///
scale(h) df(6) bhazard(rate) difficult ///
tvc(yearspl1* agegroup2 agegroup3 agegroup4) dftvc(3) eform
The effect of time since diagnosis is modelled using restricted splines; stpm2 calls rcgsen to create the spline basis variables; 6 degrees of freedom corresponds to 5 internal knots (equally spaced according to the distribution of log event times) and 2 boundary knots. Paul Lambert has written a blog post on the choice of knot locations.
Additional results
We chose to present the survival curves in figure 1 without measures of uncertainty. Following are the confidence intervals for selected years.
+-------------------------------------------------+
| year agegroup usa surv5 95% CI |
|-------------------------------------------------|
| 1990 18-29 USA 0.388 0.350 0.425 |
| 1990 30-44 USA 0.247 0.212 0.283 |
| 1990 45-64 USA 0.159 0.134 0.187 |
| 1990 65-84 USA 0.071 0.053 0.091 |
|-------------------------------------------------|
| 2000 18-29 USA 0.469 0.426 0.511 |
| 2000 30-44 USA 0.354 0.311 0.396 |
| 2000 45-64 USA 0.243 0.212 0.276 |
| 2000 65-84 USA 0.084 0.064 0.109 |
|-------------------------------------------------|
| 2010 18-29 USA 0.570 0.515 0.622 |
| 2010 30-44 USA 0.516 0.461 0.569 |
| 2010 45-64 USA 0.359 0.321 0.396 |
| 2010 65-84 USA 0.174 0.140 0.211 |
|-------------------------------------------------|
| 2015 18-29 USA 0.622 0.531 0.700 |
| 2015 30-44 USA 0.601 0.513 0.678 |
| 2015 45-64 USA 0.422 0.359 0.485 |
| 2015 65-84 USA 0.250 0.187 0.318 |
|-------------------------------------------------|
| 1990 18-29 Sweden 0.437 0.358 0.513 |
| 1990 30-44 Sweden 0.262 0.199 0.329 |
| 1990 45-64 Sweden 0.190 0.144 0.240 |
| 1990 65-84 Sweden 0.068 0.043 0.100 |
|-------------------------------------------------|
| 2000 18-29 Sweden 0.625 0.539 0.699 |
| 2000 30-44 Sweden 0.351 0.271 0.431 |
| 2000 45-64 Sweden 0.276 0.218 0.336 |
| 2000 65-84 Sweden 0.084 0.053 0.123 |
|-------------------------------------------------|
| 2010 18-29 Sweden 0.691 0.606 0.761 |
| 2010 30-44 Sweden 0.560 0.470 0.640 |
| 2010 45-64 Sweden 0.417 0.337 0.495 |
| 2010 65-84 Sweden 0.155 0.108 0.211 |
|-------------------------------------------------|
| 2015 18-29 Sweden 0.705 0.564 0.808 |
| 2015 30-44 Sweden 0.668 0.536 0.770 |
| 2015 45-64 Sweden 0.495 0.366 0.612 |
| 2015 65-84 Sweden 0.211 0.129 0.308 |
+-------------------------------------------------+
Sensitivity analysis for number of knots
We evaluated a series of choices for both the number of knots and the knot locations for the spline variables. Following are tables of AIC/BIC and predicted curves for a selection of choices.
[To be completed]
Sex-specific estimates
Survival was similar between males and females, but not identical. We chose to present a combined analysis for males and females. Sex specific results are shown below.
[To be completed]